Let’s simulate a Universe with a non-standard topology, namely a 3-Klein Bottle topology, consisting of the product of a circle and a Möbius strip. In such a Universe, one axis is reversed when you move around a second axis, while the third axis is periodic as usual. How would you compute long-range gravitational forces in this case?

The solution turns out to be surprisingly simple. The usual set-up for cosmological simulations is a volume \([0,1]^3\) with periodic boundary conditions, which is isomorphic to a 3-torus. If, in addition, we impose a reflective boundary condition around one of the diagonals, identifying the points \((x, y, z)\) and \((x, z, y)\), we obtain a double cover of the 3-Klein Bottle. In this representation, the bottom edge is identified with the right edge going in the opposite direction. See the image below, where the upper triangle is the mirror image of the lower triangle. The double cover is a little strange, because it means that we are simulating each point twice. However, this arrangement allows us to use Fourier methods for setting up initial conditions and computing long-range forces.

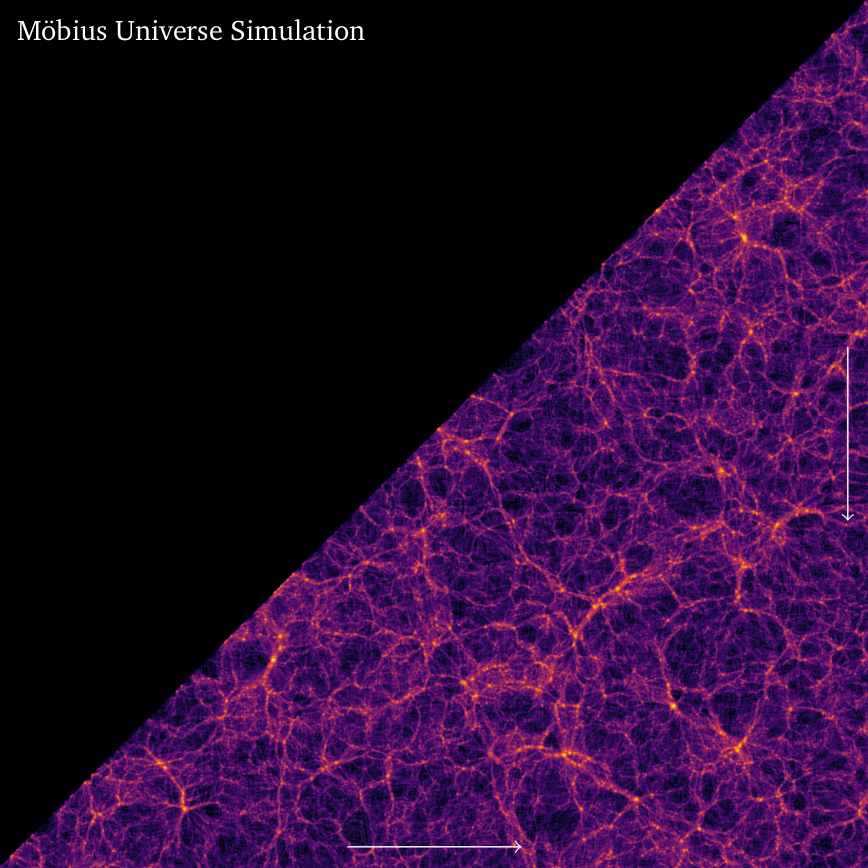
To get a snapshot that is more easily recognizable as a Klein bottle, we then discard half the volume (the upper triangle in the first image) and remap coordinates such that the bottom edge and right edge lie at opposite ends.

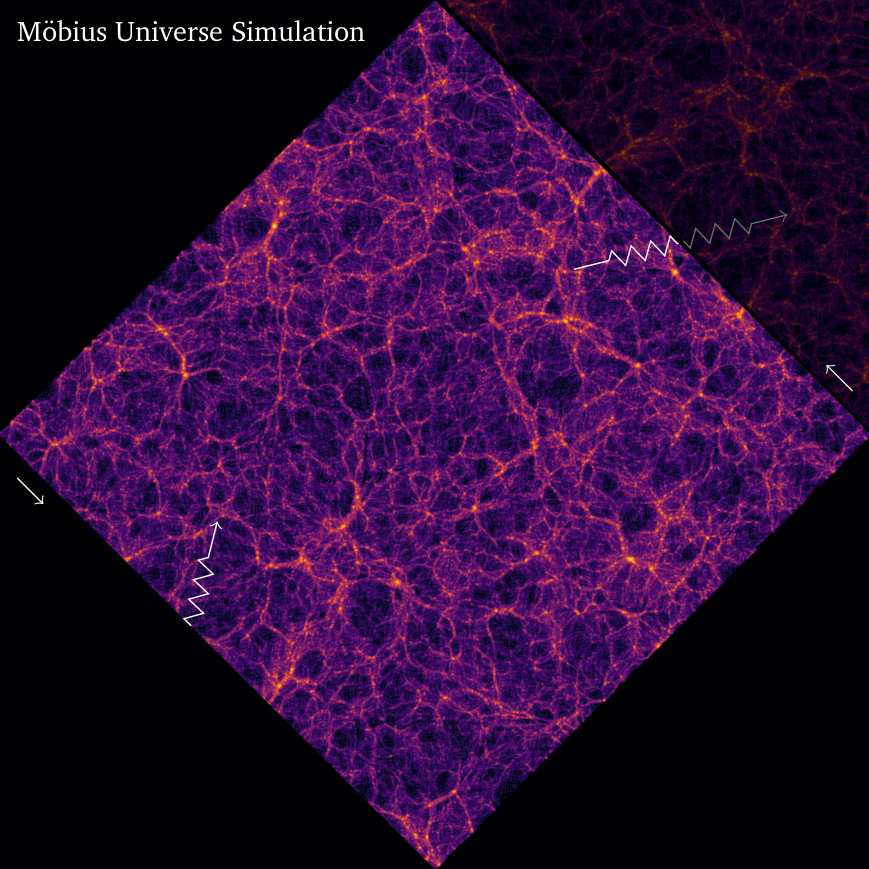
Here, I’ve the drawn the trajectory of a particle traversing the length of the Möbius strip (the zig-zag line). The transparent image in the top-right shows what we would expect for the usual topology. Instead, the particle finds that the Universe is mirrored and the prominent filament that was to its left… is now to its right.

Note that the other two edges (top-left and bottom-right) are not identified. They correspond to two halves of the reflective boundary from the first image. A particle approaching either of these edges would simply reflect back.