The following packages can be used to compute the persistent homology from a point cloud:
Our Field Filtration and Radial Filtration methods are available here:
- FieldFiltrations (uses CGAL and GUDHI)
In addition, you can use our fork of the HERA code to calculate the Frechet average and variances of persistence diagrams:
- HERA (use geom_matching/wasserstein/frechet_average after building)
Background
In topology, homology provides us with a description of an object in terms of its holes. In three dimensions, we distinguish holes in dimensions 0, 1, and 2. A 0-dimensional hole is a gap separating different components. A 1-dimensional hole is a tunnel that can be encircled by a loop. A 2-dimensional hole is a void enclosed by a shell.
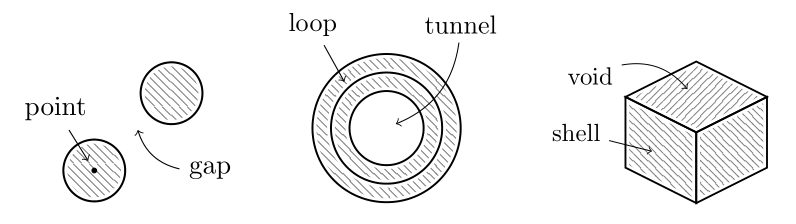
Holes and loops in dimension k=0, 1, 2.
By computing the homology of a filtration (a sequence of growing/shrinking objects), we can study how the topology changes as we vary some filtration parameter α. For example, one can study how the superlevel set of a field evolves as one lowers the threshold from +∞ to –∞. In our paper (Elbers & van de Weygaert, 2018), we consider growing bubble networks modelled as balls in R3 with increasing radius.

Filtration produced by taking superlevel sets of a 2D field. Source: Pravav et al. (2017).
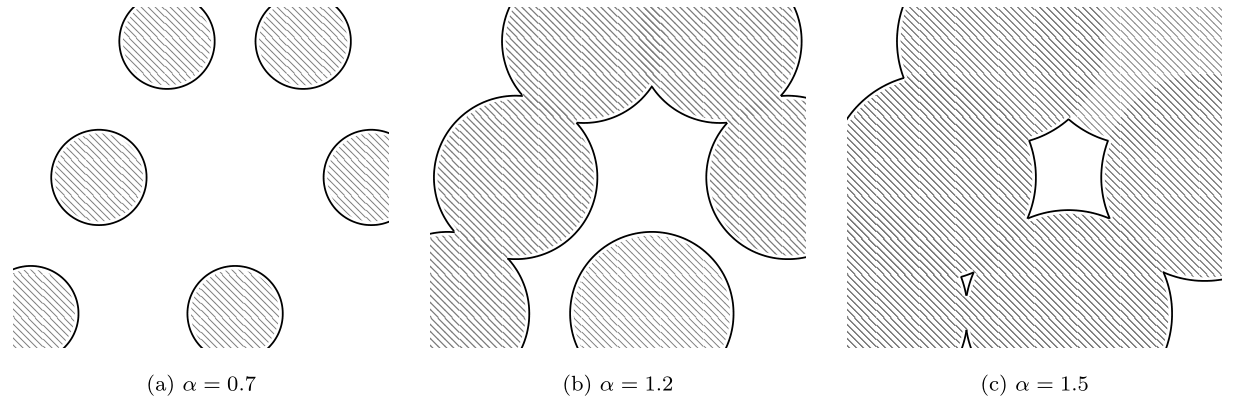
Filtration produced by inflating balls, representing a bubble network.
In both examples above, we see the death of multiple gaps as components merge. In the top example, we also see the birth and death of a tunnel. In the bottom example, we see the birth of two tunnels in the final panel.
Recall that α is the filtration parameter. We assign every hole a birth scale αbirth and death scale αdeath at which the hole appears and disappears, respectively. The difference αdeath – αbirth is the persistence of the hole. We can plot the (birth, death)-pairs in a persistence diagram. The horizontal/vertical distance from the diagonal is the persistence.
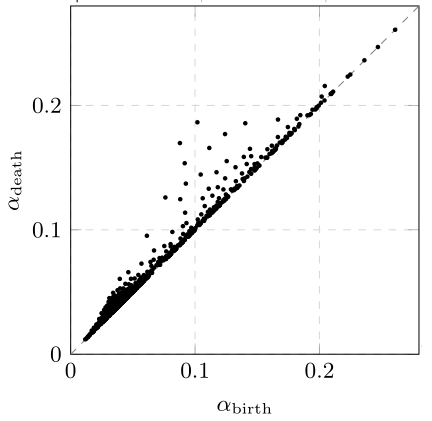
A persistence diagram shows the births and deaths of holes as a function of the filtration parameter α.